Constant Velocity
While the term “velocity ripple” is commonly used, and often appears in application requirements, it is somewhat misleading, and we prefer other measures to characterize stage performance.
In general, the need to move at constant velocity arises because a customer action occurs at a fixed frequency, and their goal is to have the result occur at uniform position intervals on some moving product. Clearly, if we can move at a perfectly constant velocity, this goal will be achieved. It should be noted that modern motion control electronics generate velocity command profiles using digital circuitry locked to precise crystal oscillators. As a result, the commanded motion profiles generated by these controllers are essentially perfect; virtually all of the velocity ripple measured in moving stages is due to the stage failing (for a wide variety of reasons) to follow the controller’s commanded motion profile accurately. Over long periods of time, the average velocity error will be that of the crystal oscillator, which is typically accurate to better than 0.01%. More typically, the challenge is to provide velocity uniformity on time scales ranging from a few milliseconds to a minute, and in this case the crystal accuracy is only one of a number of sources of velocity error.
 In a fair fraction of applications, the “fixed frequency” customer process is fixed simply because it is triggered by a digital strobe signal. This is typically provided by a crystal oscillator, which is an obvious and simple choice, provided that a positioning system vendor can be found who can provide a “perfect” constant velocity stage. Since perfection is potentially costly to attain, we frequently recommend a fairly low cost alternative: add a linear encoder to the positioning stage, and derive a digital strobe from the actual position of the product, as opposed to a crystal-based clock. In this case, variations in the speed of the positioning stage are irrelevant, and the spatial position of the customer action on the product will be extremely uniform. With the use of digital PLDs and/or PLLs, fairly arbitrary ratios between encoder resolution and event spacing can be accommodated. A typical application for which this works very well would be a laser marking system, for which laser pulses must occur at specific intervals on a part. In certain optical scanning applications, this approach is considered unacceptable, since features will be overexposed if the stage were to slow down at any point. Some of these applications can also use this technique, however, if their light source is capable of high-speed modulation. In this case, the illumination can be turned on and off so as to allow a fixed integration period for the detector, irrespective of changes in stage velocity. Since the strobes to the detector A:D system originate from the linear encoder, position uniformity of the samples is also assured. All of this is to say that in many cases, applications do not need constant velocity, and a better system architecture may allow the use of a lower cost stage with easily measurable “velocity ripple”. We’re not trying to duck the technical challenge here, but merely to save the customer money. We’re not trying to duck the technical challenge here, but merely to save the customer money.
In a fair fraction of applications, the “fixed frequency” customer process is fixed simply because it is triggered by a digital strobe signal. This is typically provided by a crystal oscillator, which is an obvious and simple choice, provided that a positioning system vendor can be found who can provide a “perfect” constant velocity stage. Since perfection is potentially costly to attain, we frequently recommend a fairly low cost alternative: add a linear encoder to the positioning stage, and derive a digital strobe from the actual position of the product, as opposed to a crystal-based clock. In this case, variations in the speed of the positioning stage are irrelevant, and the spatial position of the customer action on the product will be extremely uniform. With the use of digital PLDs and/or PLLs, fairly arbitrary ratios between encoder resolution and event spacing can be accommodated. A typical application for which this works very well would be a laser marking system, for which laser pulses must occur at specific intervals on a part. In certain optical scanning applications, this approach is considered unacceptable, since features will be overexposed if the stage were to slow down at any point. Some of these applications can also use this technique, however, if their light source is capable of high-speed modulation. In this case, the illumination can be turned on and off so as to allow a fixed integration period for the detector, irrespective of changes in stage velocity. Since the strobes to the detector A:D system originate from the linear encoder, position uniformity of the samples is also assured. All of this is to say that in many cases, applications do not need constant velocity, and a better system architecture may allow the use of a lower cost stage with easily measurable “velocity ripple”. We’re not trying to duck the technical challenge here, but merely to save the customer money. We’re not trying to duck the technical challenge here, but merely to save the customer money.
There is a subset of the complete range of constant velocity applications for which the above techniques will not suffice. These typically involve a scanning measurement system in which a continuous illumination source cannot be modulated, or a component with inertia is in the customer process, examples of which are a high speed rotating monogon and polygon in optical scanning applications. In this case, there is no ability to slow down or speed up the polygon to match variations in the speed of the positioning stage. In these applications, it is in fact important that our stage move at a constant velocity. The concept of “velocity ripple”, however, is not the best way to characterize stage performance. To better visualize this, consider a typical application, in which a customer process is writing optical data onto (or reading optical data from) a moving medium. In this case, the requirement is that the stage meet a “20 mm/sec velocity, ±1%” specification.
If we were to plot velocity vs. time, we would obtain a straight line (Figure 14a), with the dotted lines representing the ±1% tolerance. The resulting plot of position vs. time is a simple straight line whose slope is the velocity, but the effect of two “legal” 1% variations are quite different (Figure 14b). The high frequency perturbation produces a small change in the intended position trajectory, while the position error of the low frequency perturbance is quite large. Since most applications of this sort cannot directly sense any of the derivatives of position, it is the position error that matters.
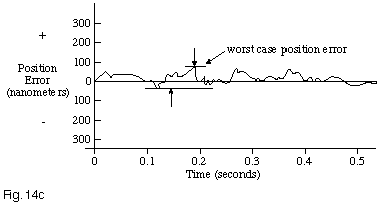
Accordingly, we prefer to measure position directly, using laser interferometers with resolutions of up to 1.25 nanometers and sampling rates of up to 100 kHz. When plotted, the result is a nearly perfect straight line whose slope equals the velocity. To better see the deviations from the intended position trajectory, we then subtract a best-fit straight line to the data and greatly increase the position sensitivity, providing a graph of Position Error versus Time. (Figure 14c).
This is the most physically significant means of representing the data, and it reveals the deviation from the intended position trajectory at any given time. For further analysis, we perform FFTs on both the position and velocity vs. time data, and analyze the spectral content of the data. This can identify structural resonances to modify via design changes, as well as suggest the appropriate frequencies at which to implement notch filters, to further suppress positional error. In some cases, we convolve the resulting spectral content against a customer-provided weighting function, and then transform back into position domain to see the position error through the filter of the customers’ sensitivities. For those applications where stage velocity is actually significant, our Zygo laser interferometer performs a “time-stamping” of position data, such that the time of each position measurement is known to an accuracy of 16 nanoseconds. Together with its resolution of 1.25 nanometers and sample rate of up to 100 kHz, this is a powerful tool for analyzing stage dynamics.
Stage design for constant velocity systems (again, we prefer to think in terms of “deviation from intended position”) must be based upon an understanding of root causes. These causes are different depending upon the basic conformation of the stage; whether the stage is leadscrew or linear motor driven, uses stepping or servo motors, has recirculating, non-recirculating, or air bearing ways, etc. The paragraphs below describe some of the root causes for various stage conformations.
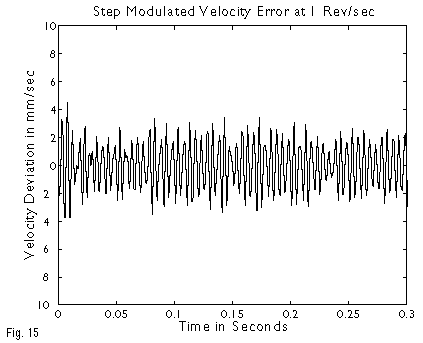
Stepping motors have an inherently discrete mode of operation that can cause velocity ripple at the motor step rate, especially at lower rates. Microstepping can greatly reduce this. In Figure 15a, the primary source of velocity error is caused by individual full steps.
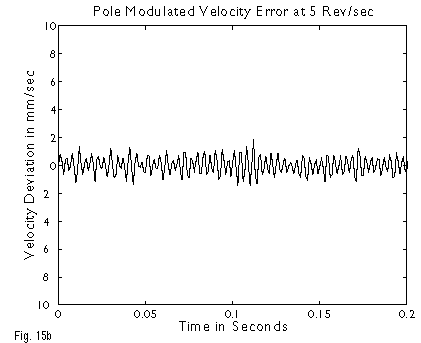
Above the motor’s primary resonance (~1 revolution/second) the ripple amplitude driven by step rate falls off rapidly, until, at intermediate speeds (~5 revolutions/second) the effects of individual steps disappear, to be replaced with a component dominated by the manufacturing tolerances of the stepping motor’s 50 magnetic poles (Figure 15b). Microstepping cannot reduce this effect. At still higher speeds (~25 revolutions/second), as pole modulation exceeds 1 KHz, it is swamped by the system’s mechanical inertia, and no longer produces a signature. This leaves a residuum of velocity ripple due to leadscrew periodic error and torque variation, as well as the fine structure of the bearings and ways.
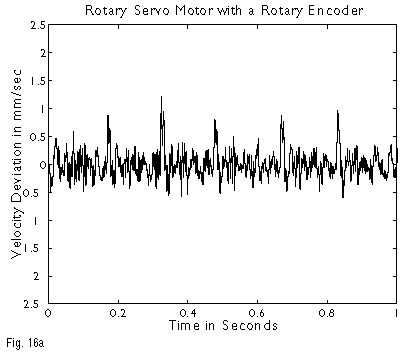
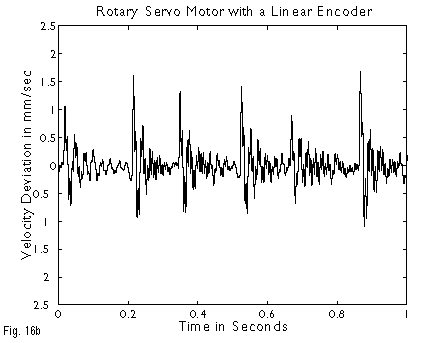
Servo systems using leadscrews with rotary encoders for position feedback exhibit measurable levels of velocity ripple, synchronous with leadscrew rotation. Some of this error may be attributed to leadscrew pitch variation. In addition, since servo systems typically have lower torsional stiffnesses than steppers do, they exhibit variable following error (and, hence, velocity ripple) due to leadscrew torque variation. The use of linear encoders avoids errors due to leadscrew pitch variation, but the decoupling of the motor and encoder due to compliance in the leadscrew, nut, stage, and encoder read head introduces phase shift into the servo loop, necessitating a lower servo bandwidth. Lower servo bandwidth decreases the torsional stiffness of the servo system, and may increase errors due to leadscrew torque variations. In both Figures 16a and 16b, the larger spikes are due to the use of Hall Sensors for digital commutation. Sinusoidal commutation (described below) can eliminate this effect.
Stages using recirculating way bearings exhibit noticeable force variation due to ball exit/entrance, which will cause velocity “spikes” at random intervals as the stage moves. In linear motor driven stages, which typically have much lower moving inertia than leadscrew driven stages (the moving inertia of most leadscrew driven stages is dominated by the rotational inertia of the screw, not by moving mass of the stage), this effect is particularly noticeable. For this reason, non-recirculating bearings, or, better still, air bearing ways are preferred in staging designed for extremely low velocity ripple.
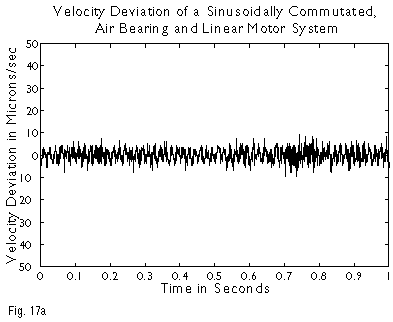
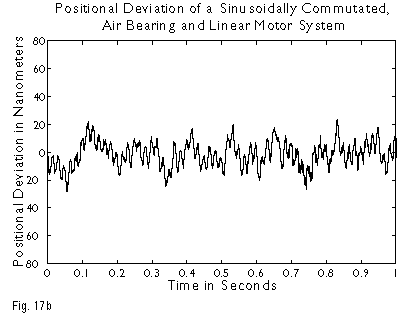
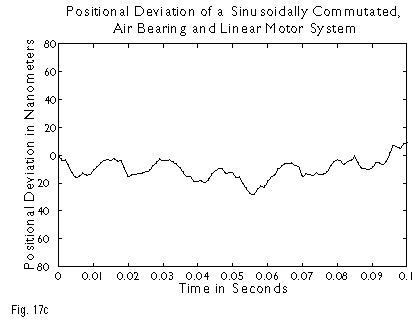
Extremely low levels of velocity ripple can be achieved using sinusoidally commutated linear motors, driving low friction rolling element or air bearing ways. Here, the residual error sources are linear motor magnetic field variations relative to an ideal sinusoidal field, variations in way friction, encoder interpolation errors, forces due to moving cables, amplifier current loop zero crossing errors, digital quantization effects in the control electronics, etc. A graph of velocity versus time for a sinusoidally commutated, linear motor/air bearing system moving at 4 millimeters/second is shown in Figure 17a. As previously mentioned, however, it is not velocity error per se that is important. Of greater interest is the resulting positional tracking error, shown in Figure 17b, with an enlarged view of a section in Figure 17c. In this case, the system is following its intended trajectory with an error of only �20 nanometers (~50 atoms)! After the stage design is optimized, custom modifications to the servo loop filter permit errors to be further reduced. At Dover, we have developed extensive experience in the design of constant velocity systems, and can configure a system to specifically address the technical and budgetary needs of your application.