Torque and Force Requirements
Torque is required to both overcome friction in the nut, and accelerate the motor and load to the required top speed.
Similarly, in linear motor applications, force is required to overcome friction in the ways, cable bending forces, and to accelerate the moving mass of the stage and the user payload. In general, calculations of this sort make the most sense (and are a lot easier) when the MKS system of units is employed. The MKS unit of torque is the Newton-meter (N-m), and the corresponding unit of rotational inertia is kilogram-meters squared (kg-m2).
Rotary Motor Example
The load which must be accelerated consists of the manual positioning knob, the motor rotor, the flexible shaft coupling, the leadscrew, the moving portion of the positioning table, and the user payload. The rotational inertia (J) of the knob used on DOVER positioning tables is 6.3 x 10-6 kg-m2 while the helical shaft coupling has an inertia of 2.2 x 10-6 kg-m2. The rotor inertia varies with motor frame size and length. Specific values of the rotor inertia for six standard motors are as follows:
Rotor Inertia
Stepping Motors:
17 frame, 0.16 N-m (23 oz-in) holding torque:3 x 106kg-m2
23 frame, 0.38 N-m (50 oz-in) holding torque:11 x 106kg-m2
23 frame, 0.71 N-m (100 oz-in) holding torque:23 x 106kg-m2
Servo Motors:
40 mm square brushless:5.65 x 106kg-m2
50 mm square brushless:38.1 x 106kg-m2
Brush servomotor:26.1 x 106kg-m2
Depending on size, our tables can be provided with either ~12 mm or ~18 mm outer diameter (OD) leadscrews, whose rotational inertias are 2.7 x 10-6 and 1.2 x 10-5 kg-m2 per 100 mm of travel, respectively. The process of determining the required torque for a given application begins by adding the rotary inertia of the knob, motor rotor, coupling, and leadscrew. The user payload mass and the moving mass of the positioning table must then be summed, and converted into an equivalent rotary inertia, via the following formula:
Rotational Intertia of Table & Load
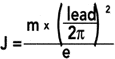
J: rotational inertia, in kg-m2
m: total moving mass, in kg
lead: screw lead, in m
e: screw efficiency
The efficiency of the leadscrew is typically 0.6 for our leadscrews with anti-backlash nuts, and 0.9 for ballscrews. The moving masses of single-axis stages, as well as the upper and lower axis moving masses for X-Y tables, are listed with the specifications for each table. Finally, the total rotational inertia is converted to a torque which, when summed with the friction torque, equals the total required torque. The frictional torque of DOVER positioning tables is held between 0.03 and 0.06 N-m for 12 mm OD leadscrews, and between 0.06 and 0.09 N-m for 18 mm OD screws. While the nut can be adjusted to lower torque values, this can reduce its otherwise excellent (1-2 micron) repeatability, and decrease the axial stiffness. Due to the presence of a lubricant film, the friction between leadscrew and nut increases with rpm, as well as at lower temperatures.
As an example, consider our XYL-1515-SM, a 300 mm x 300 mm (12″ x 12″) travel xy table. It is supplied with a standard motor, and has an upper axis moving mass of 8.6 kg. We will assume a screw lead of 5 mm (0.005 m), a leadscrew diameter of 18 mm, and a user payload of 23 kg. This load must be accelerated at 2 meters per second squared. To begin, we sum the rotational inertias of the respective components:
Sum of Rotational Inertias
J Coupling = 2.2 x 106 kg-m2
J Motor = 23 x 106 kg-m2
J Leadscrew = 12 x 106 kg-m2 x (300mm/100mm) = 36 x 106 kg-m2
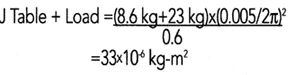
Total Rotational Inertia = 1.0 x 10-4 kg-m2
Note that the rotational inertia of the leadscrew is greater than that of the payload.
The formula to convert rotational inertia to torque is as follows:
Torque
T: torque, in N-m
J: rotational inertia, in kg-m2
A: acceleration, in m/s2
Lead: screw lead, in m/rad
In this case,
![]()
(Remember, a Newton is a kg-m/s2). Summed with a frictional torque of 0.09 N-m, this results in a total torque requirement of 0.34 N-m. This is less than the motor’s holding torque of 0.70 N-m. However, motor torque falls off with speed; the intersection of the torque requirement with the motor’s speed-torque curve determines the maximum speed to which this load could be accelerated without stalling (about 22 revolutions/second in the above case, using a DOVER 310M). The increase in frictional torque at 22 revs/second due to lubricant viscous drag will reduce this achievable top speed, to perhaps 12 revs/second. Adopting a safety margin of 20%, operation at speeds of up to 10 revolutions per second would be acceptable. Lowering the acceleration will reduce the torque requirement, allowing higher speeds to be obtained, but at an increase in overall move duration. The speed-torque curve for a given motor is a function of the drive design and operating voltage.
The foregoing rotary motor example provides specific numerical relationships between the inertia of various table components, and the formulas relating inertia to required torque. The degree of exactness may prove misleading; a variety of small, hard to quantify effects, including lubricant viscosity, nut pitch vs. efficiency, etc., conspire to defeat a purely quantitative approach to load and motor sizing. In particular, opinions vary as to what constitutes an acceptable safety margin for step motor systems, which may range from 10 to 30 percent. Whenever possible, actual simulation of the application is recommended before committing to a set of performance criteria. Vertically oriented applications, for example, alter nut efficiency in a manner difficult to predict in advance. At DOVER, we regularly “get the lead out”, setting up dummy loads and duplicating a proposed configuration as closely as possible. Consultation with our Applications Engineers is recommended when sizing a motor to achieve specific results.
Linear Motor Example
These systems are considerably more straightforward than rotary motor based stages. Newton’s second law is just about all you need: F = m x a. The moving mass of the stage and the mass of the customer payload are added to obtain the total moving mass (in kg), which is multiplied by the desired acceleration, in meters per second squared. One “G” is 9.8 m/s squared. A moving mass of 10 kilograms and an acceleration of 5 m/s2 will require a force of 50 Newtons. To this must be added the frictional force of the ways, and any other forces, such as cable loop bending forces. If these total 10 Newtons (for a total of 60 Newtons), and the force constant of the linear motor is 15 Newtons per Amp, then the peak coil current would be 4.0 Amperes. Since the force constant and back-emf constant are the same in MKS units, the stage back-emf will be 15 volts per meter/sec. At a top speed of 0.5 meter per second, the back-emf will therefore total 7.5 volts. If our coil resistance is 4.0 ohms, we will require 16 volts to drive 4 amps through this coil (Ohms law, V = I x R), so the total supply voltage required will be 16 + 7.5 + 3 volts (for FET, cable, and connector losses), for a total of 26.5 volts.

