Motion Calculations

Most numeric questions about positioning applications boil down to one of two types: “How long does it take to get there?” and “How fast am I going (at top speed; at time t; point x; etc.)?”

The related question of whether the motor has sufficient torque or force to perform the required profile is covered under Torque and Force Requirements.

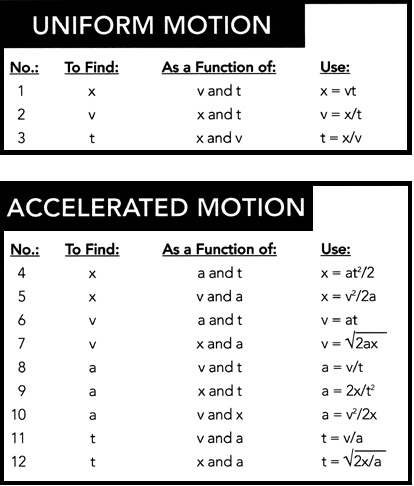
There are four physical quantities associated with motion calculations: position (x); its first derivative, velocity (v); its second derivative, acceleration (a), and of course, time (t). These quantities are related by several familiar equations, which can in turn be expanded by substitution to cover any combination. The full set of possible combinations follows.

As an example, consider the simple move profile of Figure 20. A positioning table makes a move of 100 mm (0.1 meter), accelerating at 0.2 “G” to a top speed of 400 mm/sec (0.4 m/sec), and then decelerating at 0.5 G. Since one “G” is 9.8 m/s2, the acceleration occurs at 1.96 m/s2, and the deceleration occurs at 4.9 m/s2. Using formula #11 (t=v/a), the accel time is found to be 0.204 second; using formula #5, the accel distance is found to be 40.8 mm. Similarly, the decel time and distance are found to be 0.082 second and 16.3 mm, respectively. The constant velocity distance is found by subtracting the sum of the accel and decel distances from the overall move size of 100 mm, leading to a 42.9 mm length of the move at constant velocity. Using formula #3, this phase has a duration of 0.107 second, for an overall move time of 0.393 second. If the move distance was less than 57.1 mm, and the acceleration and deceleration values were unchanged, then the stage would not be capable of reaching the 400 mm/sec top speed, and the velocity profile would be triangular, rather than the trapezoidal shape shown below.

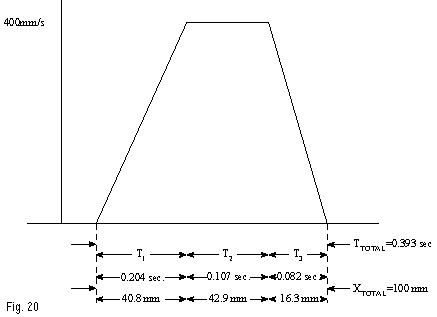
Figure 20 – Speed Profile